创建乘积数组.md

题目描述

给定一个数组A[0,1,...,n-1],请构建一个数组B[0,1,...,n-1],其中B中的元素B[i]=A[0]*A[1]*...*A[i-1]*A[i+1]*...*A[n-1]。不能使用除法

解题思路

正常来说，看到这个题目，首先想到的是B[i]中的值为A中所有数的乘积再除以A[i]，但题目规定了不能用除法。

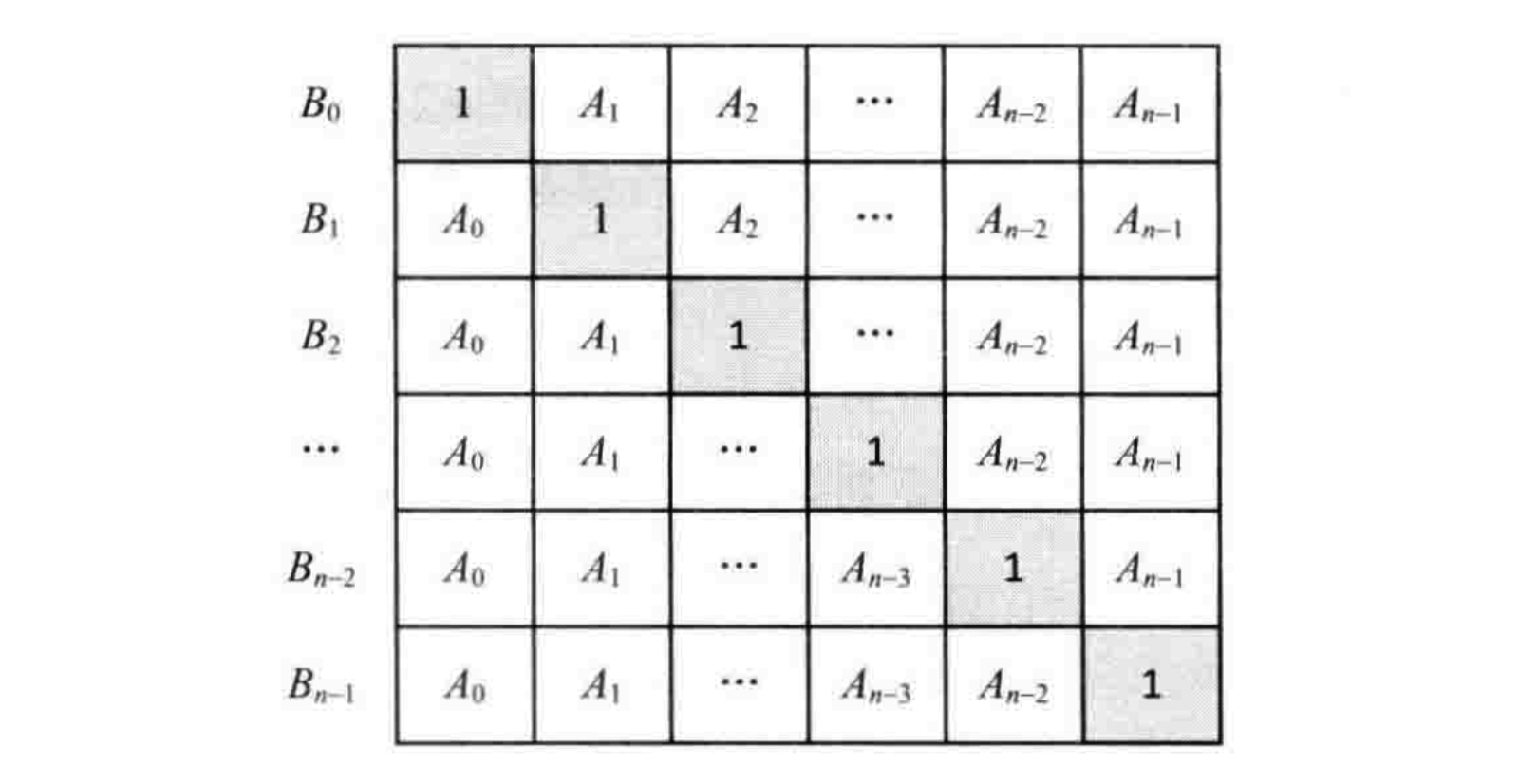
所以换一种思路，我们将B[i]的每个值都取出来，如下图：

如图，B中每一项的值为每一行的乘积；

所以我们可以分别求出下半个三角形和上半个三角形，然后乘积即为数组B

coding

function multiply (array) {
    const result = []
    if (Array.isArray(array) && array.length > 0) {
        result[0] = 1;
        for(let i = 1; i < array.length; i++) { // 计算下半三角形
            result[i] = result[i - 1] * array[i - 1]
        }
        let temp = 1;
        for (let j = array.length - 2; j >= 0; j--) { // 计算上半三角形并乘以之前的下半三角形
            temp = temp * array[j + 1] // 上半三角形的每一项
            result[j] = temp * result[j]
        }
    }
    return result
}

测试代码

console.log(multiply([1, 2, 3, 4]))
// [24, 12, 8, 6]